Abstract: Elliptic curve cryptography is a public key system that provides the highest bit strength in all public key cryptosystems currently known. When the elliptic curve cryptosystem is implemented in FPGA, the multiplication and inversion operations in the polynomial finite field based on GF(2) are two major difficulties. This paper provides an FPGA implementation structure for elliptic curve cryptography. The implementation of multiplication and inversion operations in finite field based on GF(2) is discussed and compared with the performance of software implementation. Encryption Security From the perspective of number theory, any public key cryptosystem is based on an NP (unsolvable problem), that is, for a specific problem, there is no way to find a polynomial time algorithm to solve the problem. Generally, the algorithms for solving such problems are exponential time or sub-exponential time. For example, the commonly used RSA algorithm is based on the intractability of large integer factorization. After nearly 30 years of research, although the RSA algorithm does not have a polynomial time algorithm, it can find the sub-exponential time algorithm. At present, the key length must be greater than 1024 bits to ensure the security of information transmission, and the elliptic curve encryption system. (EllipTIc Curve Cryptosystem—ECC) is a public key system that can provide the highest bit strength (Strength-Per-Bit) in all public key cryptosystems. It only needs 160 keys to achieve 1024-bit RSA algorithm. The level of security provided. It is based on the Discrete Logarithm Problem (ECDLP) in a group of points on an elliptic curve over a finite field, which many cryptographers consider to be exponential. Therefore, for the elliptic curve cryptosystem, this point is analyzed from the perspectives of calculation amount, processing speed, storage space and communication bandwidth. The elliptic curve cryptosystem has great advantages. The public key encryption algorithm standard P1363 that IEEE has developed is based on the ECC algorithm. Nowadays, the cryptography community generally believes that it will replace RSA as a universal public key cryptography algorithm, which has become a research hotspot and a promising research direction. Elliptic Curve Encryption Elliptic Curve Introducing the Non-supersingular elliptic curve Weierstrass equation E: Y2+XY=X3+aX2+c where a, c∈GF(2k), c≠0. To simplify the subsequent operations, introduce z such that X = x / z; Y = y / z, then the elliptic curve equation is E: y2z + xyz = x3 + ax2z + cz3, define (x, y, z) = λ ( x, y, z). It can be seen that when z ≠0, (X, Y) and (x, y, z) correspond, when z = 0 can be understood as going to infinity along the y axis, defined as the infinity point O. Then all the points on the elliptic curve plus the set of infinity points constitute an Abel group, and O is a unit element (zero element). Two kinds of point operations are defined on the elliptic curve E: point operation and point operation. In the elliptical encryption system that has been put into use in the elliptical encryption system, most of the key lengths are relatively short, generally concentrated in 30 to 60 bits. This is because, in software implementation, the key is limited due to the software execution rate. The rate of an elliptical encryption system with a relatively large length (≥160) will not meet the usage requirements. At the same time, in hardware implementation, an elliptical encryption system with a relatively large key length will consume a lot of hardware resources. With the deep research of elliptical encryption algorithms and the rapid development of programmable logic devices, it is already a possible choice to implement elliptical encryption systems with programmable logic devices. An implementation scheme will be introduced below, and implemented by software and hardware respectively. * Multiplication of composite finite fields: Taking GF((24)2) as an example, the multiplication and addition of GF(24) can be used to construct the multiplication of GF(28). The primitive polynomial of subfield GF(24) is Q(y)=y4+y+1, and the primitive polynomial of the second subfield is R(z)=z3+z+ω14, where ω is GF(24) The base element satisfies Q(ω)=0. The multiplication of two elements in the domain [a0+a1z]&TImes;[b0+b1z] can be expressed as: Thus, the multiplication of GF((24)2) on the composite domain can be obtained by mathematical operations of the finite field on GF(24). Conclusion Public key cryptosystems are often used for key management, key exchange, digital signatures, and authentication, etc., because of their high computational complexity and time complexity. At present, the widely used algorithms such as DES and RSA are still widely used. The update of the algorithm not only can make the original password users get better performance, but also can make the IC card, mobile phone and other fields that are difficult to implement the cryptographic algorithm can be used. Password technology to ensure information security. Pouch Cell,Lithium-Ion Pouch Cell,Lifepo4 Pouch Cell,Lithium Battery Pouch JIANGMEN RONDA LITHIUM BATTERY CO., LTD. , https://www.ronda-battery.com
Figure 1 point algorithm implementation 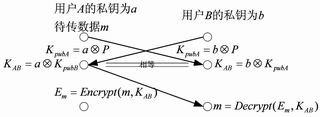
Figure 2 Key, data exchange 
Figure 3 Elliptic curve encryption system structure 
Figure 4 Block diagram of the FPGA circuit module of the elliptic curve encryption system 
Figure 5 Verifying the system structure
1) The point operation on the elliptic curve is defined as: Let P = ( x1, y1, 1) ∈ E, Q = ( x2, y2, 1) ∈ E, -P = ( x1, y1 + x1, 1), when Q≠-P when PQ=(x3, y3, z3) Then when P≠Q:
Where A=(x2z1+x1), B=(y2z1+y1), C=A+B, D=A2(A+a2z1)z1BC
When P=Q:
among them
2) The point operation on the elliptic curve is defined as: Let P = (x1, y1, 1) ∈ E, (ltlt-1...l0) 2 be a binary representation of the integer l, lP = PPAP = Q and Q ∈ E.
Using the above point operation, the point algorithm is implemented as shown in Figure 1. Define l=logpQ. If the period of P is very large, it is easier to use Q and L to find Q. However, it is difficult to use P and Q to find l. This is ECDLP. Elliptic curve encryption is built on this problem. on.
Encryption System In the Diffe-Hellman public key system, the specific elliptic curve, the point P on the curve, and the periodic prime number N of the P are all public information.
A and B want to communicate, first get elliptic curve E, point P and prime number N. User A then uses the randomly selected integer a in [1, N-1] as the private key, and A transmits KpubA=aP as its own public key to User B, while B will randomly [[1, N-1] The selected integer b is used as the private key, and KpubB=bP is transmitted to A as its own public key. A and B each multiply their own private key point by the public key passed by the other party to obtain KAB, thus completing the key exchange process. When user A needs to transmit the data to be transmitted to user B, A generates Em by using m and KAB. When user B obtains Em, the KAB generated by the key exchange process and the encrypted data Em obtained from user A are generated. Data m. See Figure 2.
According to the requirements of the above ellipse encryption system, the structure diagram of the encryption system of FIG. 3 is designed, wherein the ellipse encryption system parameter interface obtains basic parameters of the ellipse related to encryption, such as a private key, an elliptic curve, a given point on an elliptic curve, and the like. The elliptic curve multiplication control part is mainly responsible for how to calculate the multiplication result, and will call PP and PQ a lot to realize the multiplication function; and PP and PQ get the result by the finite field addition, multiplication and inversion.
Software Model Verification The main purpose of software implementation is to establish a verification model for hardware implementation. The structure of the entire software is shown in Figure 3. In the implementation of the software verification system, the addition on the finite field is an exclusive OR operation. Multiplication and inversion on a finite field are key points, and resource consumption in hardware implementation must be considered in advance, requiring efficient algorithms. In this system, the speciality brought by the composite domain GF((2n)m) is used, and the multiplication and inversion operations can be realized efficiently and quickly.
* Multiplication on GF(2n): A(y) & TImes; B(y) = C(Y) modQ(y), Q(y) is an approximate polynomial. Commonly used are: Paar-Rosner multiplier, Mastrovito multiplier, Massey-Omura multiplier, Hasan-Bhargava multiplier, etc. Here are two options:
1) When n is relatively small, it can be realized by look-up table method. Let ω be the primitive root of Q(y)=0, then F2n={0,ω,Aω2n-1}, and obtain the order of A and B by using the look-up table method. The order of a, b, and C is c=a+b, and C is obtained by c again using the look-up table method. This method is used in this system to implement multiplication on GF(2n).
2) When n is large, the resource consumption is too large and unbearable by using the look-up table method. C=Z&TImes; B (n is relatively large), Z is a matrix determined by A(y), Q(y). among them:
* Inverse operation of the composite finite field: the inverse of the element A in the composite finite field GF((2n)m) is:
Among them, it can be observed that Ar belongs to an element in the sub-domain GF(2n), and the value of (Ar)-1 can be easily obtained.
FPGA hardware implementation The software development method has a short development time, but its encryption speed is slow, which hinders the practicability of elliptic curve encryption. The FPGA approach combines software flexibility with hardware security to provide superior speed over software-based methods. Compared to traditional ASIC implementations, programmable devices are more suitable for cryptography applications due to their high degree of flexibility. field.
Based on the software model, we optimized the model for the characteristics of the FPGA hardware. According to the requirements of the elliptic curve encryption algorithm, the encryption system is modularized, each module independently completes its respective functions, and the modules exchange data and sequence control to achieve the encryption function. Figure 4 is a block diagram of the circuit block of the elliptic curve cryptosystem FPGA implementation.
Among them, the elliptic curve encryption control system module is the core of the whole system. When Ready is True, the system reads in the initial data and controls the RAM to store the initial data. In the operation process, the module performs a control loop on the selector according to the data source, performs PP=R and PQ=R operations, obtains the final result, and then outputs the result through the Out_Ready signal; the selector module according to the instruction provided by the control system module The PP=R module and the PQ=R module are controlled, and corresponding real-time data streams are provided; the PP=R module and the PQ=R module perform timing control on the addition and multiplication operations on the finite field to obtain points on the elliptic curve. The addition operation will directly affect the speed performance of the whole system, so it is necessary to design a reasonable input and output data stream for the addition and multiplication operations on the finite field to achieve a high efficiency operation rate. Various memory modules store the initial values ​​of the system, the intermediate values ​​in the operation process, and the system operation results according to different instructions.
Based on the above various factors, we chose XILINX's VirtexII device, ISE 4.1 as the development platform, and VHDL as the development language. Since the calculation of the 168-bit elliptic curve cryptography algorithm is relatively large, wiring is a factor worth considering when implementing the FPGA. The choice of FPGA devices should take into account routing resources, and the Virtex family offers a wealth of routing resources. After the simulation on Modelsim, the performance index is: the initial setup time is required for the first encryption or decryption under the 40MHz clock drive. The output of the plaintext or ciphertext needs about 2ms, and the output of the plaintext or ciphertext is about 25Mbps. It can be seen that this is a relatively high rate and can be applied to many occasions.
Application System Verification After the ellipse encryption hardware is implemented, it must be verified in the actual system. We specially constructed a serial port encryption experiment board for verification. The structure of the whole verification system is shown in Figure 5. After the actual system verification, the hardware implementation of the elliptical encryption system is proved to be successful.
The elliptic curve cryptosystem (ECC) is attracting the attention of the industry with its shorter key and theoretically higher strength, and the hardware implementation of the elliptic curve cryptosystem (ECC) will also be a focus point in the public key cryptosystem. . Although this paper has laid a good foundation for future work, there is still a lot of work to be done in the following aspects. The first is the development of programmable logic devices. In the future, there will inevitably be devices that can provide a larger number of gates and provide faster rates. Secondly, the improvement of the elliptic curve cryptosystem itself; finally, the further improvement of the hardware implementation algorithm of finite field mathematical operations. With the development of all the above aspects, hardware implementations that provide longer keys and faster data rates will provide faster and more secure encryption systems for national economic and social development.