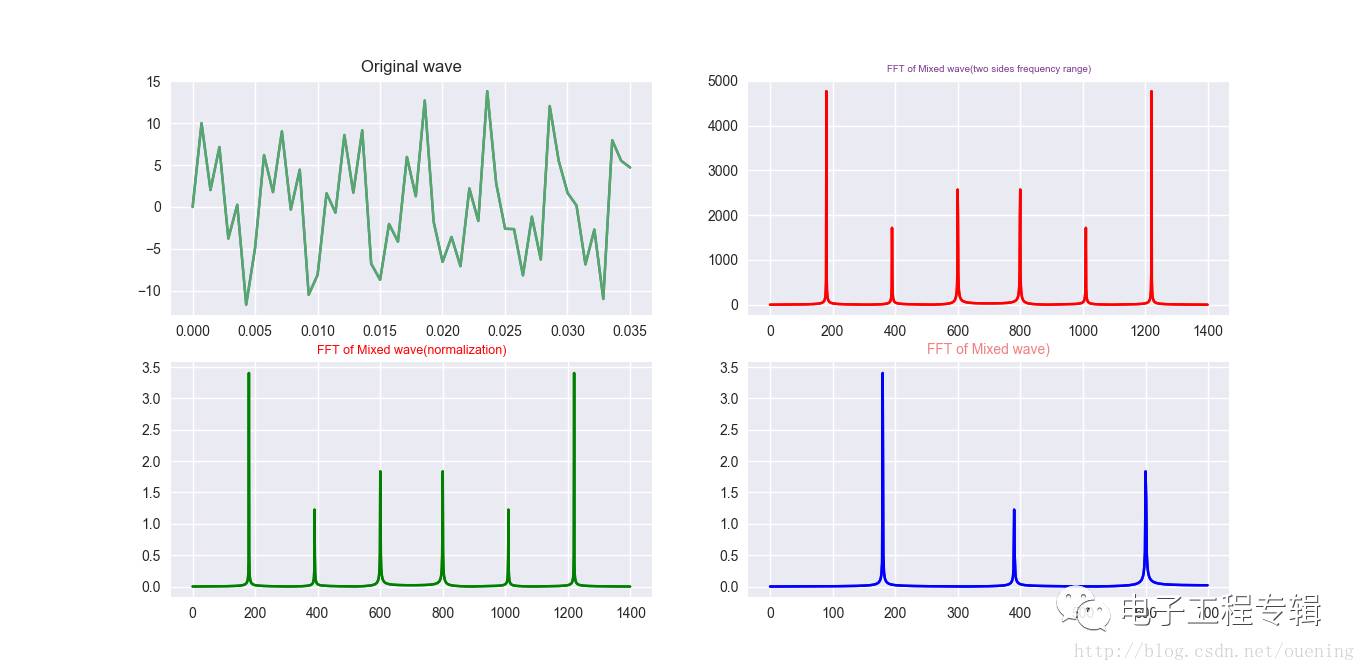
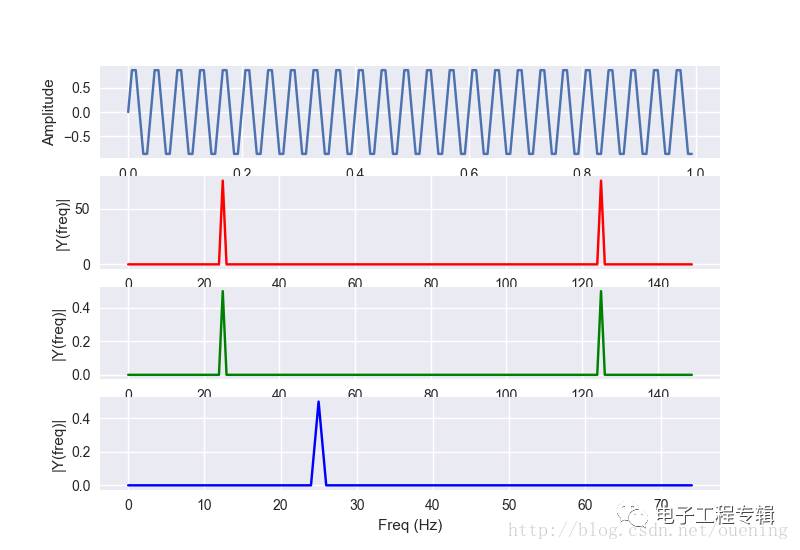
Here is a recorded example of Fast Fourier Transform (FFT) implementation. This code does not provide an in-depth explanation of FFT but includes detailed comments for clarity. The script uses NumPy, SciPy, and Matplotlib to perform the FFT on a signal composed of three different frequencies: 180 Hz, 390 Hz, and 600 Hz. According to the Nyquist sampling theorem, the sampling frequency must be at least twice the highest frequency component in the signal. Therefore, we set the sampling frequency to 1400 Hz, which gives us 1400 samples per second. The code starts by generating a time vector with 1400 points, then constructs the signal as a sum of sine waves. After performing the FFT using `scipy.fftpack.fft`, it extracts the real and imaginary parts and calculates the magnitude spectrum. To visualize the results, the code plots the original signal, the full FFT spectrum, the normalized FFT, and the single-sided frequency range. These visualizations help understand how the frequency components are distributed in the transformed domain. As a simple addition, here's another example that demonstrates FFT on a single-frequency signal. In this case, the signal is a 25 Hz sine wave sampled at 150 Hz. The code computes the FFT, normalizes the result, and plots the amplitude spectrum in different ways. It also shows the one-sided frequency spectrum, which is more commonly used in practice because the other half is redundant due to symmetry in real signals. Electronics Packaging,Microwave Power Divider,Ceramics Used In Electronics,Electronic Communications Device Shaanxi Xinlong Metal Electro-mechanical Co., Ltd. , https://www.cnxlalloys.com